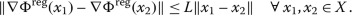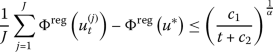- Research
- Open access
- Published:
Ensemble Kalman inversion for image guided guide wire navigation in vascular systems
Journal of Mathematics in Industry volume 14, Article number: 21 (2024)
Abstract
This paper addresses the challenging task of guide wire navigation in cardiovascular interventions, focusing on the parameter estimation of a guide wire system using Ensemble Kalman Inversion (EKI) with a subsampling technique. The EKI uses an ensemble of particles to estimate the unknown quantities. However, since the data misfit has to be computed for each particle in each iteration, the EKI may become computationally infeasible in the case of high-dimensional data, e.g. high-resolution images. This issue can been addressed by randomised algorithms that utilize only a random subset of the data in each iteration. We introduce and analyse a subsampling technique for the EKI, which is based on a continuous-time representation of stochastic gradient methods and apply it to on the parameter estimation of our guide wire system. Numerical experiments with real data from a simplified test setting demonstrate the potential of the method.
1 Introduction
The Ensemble Kalman Inversion (EKI) is a widely utilized technique for addressing inverse problems, which involve estimating unknown parameters based on observational data. EKI is particularly advantageous due to its efficiency in high-dimensional spaces and its ability to incorporate uncertainty in a straightforward manner. This method operates by evolving an ensemble of particles, which represent possible solutions, toward an optimal estimate by iteratively updating these particles using observational data. EKI is well-suited for problems where the forward model is treated as a black box, and it performs robustly in situations where the underlying distributions are close to Gaussian.
Despite its strengths, one challenge that arises in the application of EKI is the computational burden associated with high-dimensional data, such as high-resolution images. The need to compute the data misfit for each particle at each iteration can become infeasible when dealing with large datasets. To address this issue, we propose incorporating a subsampling technique into the EKI framework. This approach leverages randomized algorithms to utilize only a subset of the data in each iteration, significantly reducing computational costs while maintaining the integrity of the solution.
1.1 Application: guide wire navigation in vascular systems
Vascular diseases are a leading cause of mortality, accounting for approximately 40% of all deaths in Germany. The widespread adoption of minimally invasive procedures, such as percutaneous coronary angioplasty (PCA), is evident, with around 800,000 procedures performed annually in Germany. These interventions typically require accessing a large artery, such as the arteria femoralis, and navigating a guide wire under angiographic control toward the target lesion, often a coronary stenosis.
The navigation process of the guide wire is highly challenging and demands significant expertise to ensure a safe procedure. Improper navigation can lead to complications like dissections, which occur due to excessive mechanical stress on the vessel walls. Given these risks, there is a growing interest in robotic assistance for guide wire navigation. Such a system would need to execute navigation with minimal mechanical stress on the vessel walls, ideally remaining below a predefined threshold.
However, information regarding vessel compliance and surface friction is typically unavailable, necessitating real-time learning of these parameters during the procedure by observing the wire’s shape via angiographic imaging. By estimating and predicting the behavior of the vascular environment, it becomes possible to develop a probabilistic model that assesses mechanical stress during navigation, thereby facilitating risk stratification.
In this work, we propose a first step toward the automated control of guide wires, focusing on wire advancement within vascular structures. Using a simulation setting with force sensors for precise measurement and high-resolution imaging, we aim to estimate and predict the behavior of the vascular environment. The real-time estimation and prediction of the guide wire’s position are crucial, and to achieve this, we employ the EKI method, enhanced with a subsampling technique to manage the large volume of data from high-resolution images efficiently.
1.2 Literature overview
The Ensemble Kalman Filter (EnKF) is a well-established algorithm for solving inverse problems and data assimilation tasks, first introduced in [13]. Its popularity stems from its straightforward implementation and robust performance even with small ensemble sizes [3, 4, 19–21, 25, 31, 32]. Recently, the continuous-time limit of the Ensemble Kalman Inversion (EKI) has garnered significant attention, leading to convergence analyses in the observation space, as discussed in [5–7, 27, 28]. Achieving convergence in the parameter space typically requires the application of regularization techniques. For instance, Tikhonov regularization has been analyzed in [9] and is the regularization method chosen for our study. This form of regularization has continued to attract interest, with further analyses conducted on adaptive Tikhonov strategies and stochastic EKI settings [35]. Additionally, the mean-field limit of EKI has been explored in recent works [8, 12].
To address the computational challenges associated with classical optimization algorithms, the stochastic gradient descent method, introduced in [26], has been increasingly employed. This method is not only computationally efficient but also effective in avoiding local minima in non-convex optimization problems [10, 33]. For our subsampling scheme, we will leverage the continuous-time limit analysis of stochastic gradient descent, initially explored in [24] and further generalized in [22]. Our analysis will focus on subsampling in EKI for general nonlinear forward operators, building on previous analyses conducted for linear operators [18].
In the context of guide wire navigation in vascular systems, coronary vessels can be approximated as rigid but time-variant tubular geometries that respond to the heartbeat. For algorithmic simplicity, we adopt a basic representation of the guide wire as a cylindrical rod with a specified elasticity constant, rather than employing a more detailed guide wire model. Sharei et al. [29] provide a comprehensive overview of contemporary techniques for guide wire navigation, primarily utilizing finite element methods. These techniques include the Euler-Bernoulli beam model, the Kirchhoff rod model, and the Timoshenko beam, with a non-linear variant known as the Cosserat model. High-resolution images are utilized to accommodate the simplified model. To estimate the unknown parameters from the model, particle-based methods, such as EKI, are employed due to their demonstrated effectiveness and low computational costs.
1.3 Contributions and outline
This paper aims to advance robotic assistance for guide wire navigation in cardiovascular systems. We focus on a simplified setting and suggest a subsampling variant of the EKI to estimate the unknown parameters of the simulation and thus, improve the accuracy of predictions as well as to ensure feasibility of the EKI in large data settings. The key contributions of this article are as follows:
-
Formulation of a guide wire system with a feedback loop by high resolution images to learn the unknown parameters in the simulation.
-
Adaption of a subsampling variant of the EKI to estimate the unknown parameters with low computational costs in a black-box setting.
-
Analysis of a subsampling scheme for the EKI in the nonlinear setting.
-
Numerical experiments with real data from a wire model.
The structure of the remaining article is as follows: In Sect. 2, we introduce the mathematical model of the guide wire system as well as formulate the inverse problem to reconstruct an image via our model. We describe the EKI and present results on convergence analysis in Sect. 3; before introducing and analysing our subsampling scheme in Sect. 4. We then proceed to show an numerical experiment in Sect. 5 and complete our work with a conclusion in Sect. 6.
1.4 Notation
We denote by \((\Omega , \mathcal{A}, \mathbb{P})\) a probability space. Let X be a separable Hilbert space, and \(Y := \mathbb{R}^{{N_{\mathrm{obs}}}}\) representing the parameter and data spaces, respectively. Here \({N_{\mathrm{obs}}}\) denotes the number of real-valued observation variables, We define inner products on \(\mathbb{R}^{n}\) \(\langle \cdot , \cdot \rangle \) and their associated Euclidean norms \(\| \cdot \|\), or weighted inner products \(\langle \cdot , \cdot \rangle _{\Gamma}:=\langle \Gamma ^{- \frac{1}{2}}\cdot , \Gamma ^{-\frac{1}{2}}\cdot \rangle \) and their corresponding weighted norms \(\| \cdot \|_{\Gamma}:=\|\Gamma ^{-1} \cdot \|\), where \(\Gamma \in \mathbb{R}^{n \times n}\) is symmetric and positive definite matrix.
Furthermore, define the tensor product of vectors \(x \in \mathbb{R}^{n}\) and \(y \in \mathbb{R}^{m}\) as \(x \otimes y := x y^{\top}\).
2 Parameter estimation problem
In the context of inverse problems, the objective is to estimate an unknown parameter \(u \in X \) based on noisy observations \(y \in Y \). This relationship is modeled as:
where \(G: X \rightarrow Y \) is the forward operator that maps the parameter u to the observation space, and \(\eta \in Y \) represents the additive observational noise. In the specific application discussed later, the observations y correspond to high-resolution images of a guide wire, and the dimensionality of the data space Y is \(\mathbb{R}^{{N_{\mathrm{obs}}}}\), where \({N_{\mathrm{obs}}}\in \mathbb{N} \).
Within a Bayesian framework, both the parameter u and the noise η are treated as independent random variables, with \(u: \Omega \rightarrow X \) and \(\eta : \Omega \rightarrow Y \). Assuming the noise η follows a Gaussian distribution \(\eta \sim \mathcal{N}(0, \Gamma ) \), the posterior distribution \(\mu ^{y} \) of the parameter u given the observation y is expressed as:
where \(\mu _{0} \) denotes the prior distribution of the parameter u, and \(Z = \mathbb{E}_{\mu _{0}} \exp (-\frac{1}{2} \|y - G(u)\|^{2}_{ \Gamma} ) \) is the normalization constant.
The central goal is to compute the Maximum a Posteriori (MAP) estimate, which serves as a point estimate for the unknown parameter. In a finite-dimensional setting, this involves minimizing the negative log-posterior. Assuming a Gaussian prior on the parameter u, such that \(u \sim \mathcal{N}(0, \alpha ^{-1/2} D_{0}) \), the MAP estimate is obtained by minimizing the following regularized objective function:

where \(\alpha > 0 \) is the regularization parameter. For a detailed discussion in the infinite-dimensional setting we refer to [11, 23].
2.1 Wire model as forward model
To model the guide wire, we utilize Cosserat rods, which are commonly employed to simulate the dynamic behavior of slender, flexible structures that can bend, twist, stretch, and shear. Understanding the dynamics of such objects is crucial, as they are prevalent in both natural and engineered systems, including polymers, flagella, snakes, and space tethers. A comprehensive and practical numerical implementation of Cosserat rods is detailed in [16] and [36]. While we provide a brief overview of the model and the variables we use, we refer readers to these sources for a more in-depth explanation. Additionally, we make use of the mathematical software Pyelastica [30] to support our simulations. The schematic plot of the Cosserat rod in Fig. 1 is based on Figure 1 in [34].
Illustration of discretization of a Cosserat rod in a simplified setting of the sinus function. We discretize the function into nodes \(r_{i}\) with reference frames \(Q_{i}\). Each reference frame consists of vectors \((d_{1i},d_{2i},d_{3i})\), where \(d_{1i}\) and \(d_{2i}\) (green and blue arrows) span the binormal plane and \(d_{3i}\) (red arrows) goes along the tangent of the of straight connection between the nodes
2.1.1 Cosserat rods
The fundamental assumption in modeling Cosserat rods is that the rod’s length \(L \in \mathbb{R}_{>0} \) is significantly greater than its radius \(r \in \mathbb{R}_{>0} \), i.e., \((L \gg r) \). The position of the rod is described by its centerline \(r(s,t) \), where \(s \in [0, L] \) denotes the position along the rod, and t represents time. The position of the rod is given in \(\mathbb{R}^{3} \).
Vectors are expressed in local (Lagrangian) frames as \(x = x_{1} d_{1} + x_{2} d_{2} + x_{3} d_{3} \), where \(d_{1} \) and \(d_{2} \) span the binormal plane, and \(d_{3} \) points along the tangent to the centerline. The local frame is defined as \(Q = \{d_{1}, d_{2}, d_{3}\} \).
The dynamics of the Cosserat rod at each cross-section are governed by the following differential equations:
-
Linear momentum
$$\begin{aligned} \rho A \cdot \partial _{t}^{2} \bar{r} = \partial _{s}\left ( \frac{Q^{T}S\sigma}{e}\right )+e\bar{f}. \end{aligned}$$(4) -
Angular momentum
$$\begin{aligned} \frac{\rho I}{e}\partial _{t}\omega &=\partial _{s}\left ( \frac{B\kappa}{e^{3}}+\frac{\kappa \times B\kappa}{e^{3}} \right )+ \left (Q\frac{\bar{r}_{s}}{e}\times S\sigma \right ) \\ &+\left (\rho I\cdot \frac{\omega}{e}\right )\times \omega + \frac{\rho I \omega}{e^{2}}\cdot \partial _{t} e+ e , \end{aligned}$$(5) -
And boundary conditions for position \(r_{i}(t=0)=r_{0}\) and velocity \(v_{i}(t=0)=v_{0}\).
The variables are: stretch ratio \(e=\frac{\mathrm{d}s}{\mathrm{d}\widehat{s}}\in \mathbb{R}\), where \(s\in \mathbb{R}\) denotes the deformed configuration and \(\widehat{s}\in \mathbb{R}\) the reference configuration, cross-section area: \(A=\frac{\bar{A}}{e}\in \mathbb{R}^{3\times 3}\), bending-stiffness matrix: \(B=\frac{\bar{B}}{e^{2}}\in \mathbb{R}^{3\times 3}\), shearing-stiffness matrix: \(S=\frac{\bar{S}}{e}\in \mathbb{R}^{3\times 3}\), second area moment of inertia: \(I=\frac{\bar{I}}{e^{2}}\in \mathbb{R}^{3\times 3}\), local orientation of the rod \(\bar{r}_{s}=e\bar{t}\in \mathbb{R}^{3}\), where t̄ is a unit tangent vector, \(E\in \mathbb{R}\) elastic Young’s modulus, \(G\in \mathbb{R}\) shear modulus, \(I_{i}\in \mathbb{R} (i=1,2,3)\) second area moment of inertia, \(\alpha _{c}=4/3\), external force \(f\in \mathbb{R}^{3}\), couple line density \(c\in \mathbb{R}^{3}\), mass per unit length \(\rho \in \mathbb{R}\), curvature of the vector \(\kappa \in \mathbb{R}^{3}\), angular velocity of the rod \(\omega \in \mathbb{R}^{3}\), shear strain vector \(\sigma \in \mathbb{R}^{3}\) and translational velocity \(\bar{v}=\partial _{t} \bar{r} \in \mathbb{R}^{3}\). Here B and S depend on \(G,E,I_{i}\) and \(\alpha _{c}\).
2.1.2 Numerical implementation
Since analytical solutions of (4) and (5) are usually not feasible, we aim to solve the differential equations numerically. For this we discretize the rod \(r(s,t)\) into a set of N nodes \(\{r_{i}(s,t)\}_{i=0,\ldots ,N}\). Furthermore, the nodes are connected through straight line segments, where each segments has its own reference frame \(Q_{j}(s,t)\) for \(j=1,\ldots ,N\). Since there are \(N+1\) nodes we have N segments. We illustrate this in Fig. 1. Then, the above introduced values are defined for either each node or each segment. At each node we consider the velocities \(v_{i}=\frac{\partial r_{i}}{\partial t}\in \mathbb{R}^{3}\), where \(r_{i}\in \mathbb{R}^{3}\) denotes the position, as well as external forces \(\bar{f}_{i}\in \mathbb{R}^{3}\) that are applied to the rod and masses per unit length \(\rho _{i}\in \mathbb{R}\) at each node. The length of each segment is given by \(s_{j}\in \mathbb{R}\). Furthermore, we have a reference length \(\widehat{s_{j}}\in \mathbb{R}\) for each segment as well as stretch ratios \(e_{j}=\frac{s_{j}}{\widehat{s_{j}}}\in \mathbb{R}^{3}\), unit tangent vectors \(t_{j}\), shear strain vectors \(\sigma _{j}\in \mathbb{R}^{3}\), angular velocity \(\omega _{j}\in \mathbb{R}^{3}\), cross section areas \(\widehat{A}_{j}\in \mathbb{R}^{3\times 3}\), bending stiffness matrices \(\widehat{B}_{j}\in \mathbb{R}^{3\times 3}\), shearing-stiffness matrices \(\widehat{S}_{j}\in \mathbb{R}^{3\times 3}\) and second moment of inertia matrices \(\widehat{I}_{j}\in \mathbb{R}^{3\times 3}\). The curvatures \(\kappa _{i}\) are integrated over some Voronoi region \(\mathcal{D}_{i}\) at each interior node \(i=1,\ldots ,N-1\). Through those definitions we can formulate the differential equations (4) and (5) for each node and segment. We refer to [16, 30, 36] for a detailed analysis.
2.2 Experimental setup
To analyze and evaluate the physical behavior of the guide wire under both static and dynamic forces, we conducted two distinct experimental setups.
In the first setup, a static analysis was performed using a Radifocus Guide Wire M Standard type 0.035” (Terumo, Tokyo, Japan), which was positioned vertically against a surface (see Fig. 2). A series of 47 images were captured at 20 mm intervals of displacement, using a Full HD webcam. This setup allowed us to observe and document the deformation of the guide wire caused by its own weight at various positions.
To evaluate the dynamic behavior of the guide wire, we designed an electrical drive system with two degrees of freedom—axial and radial—which allows precise control of both the position and speed of the wire’s movement. A diagram of this system, including its key components, is shown in Fig. 3.
The system is composed of two motors: Motor 1, which is responsible for generating axial movement and is housed within a rotor, and Motor 2, which drives the radial movement. The entire prototype is controlled by a Raspberry Pi 4, programmed using the Robot Operating System (ROS) framework to facilitate future integration with sensors and additional applications.
During the experiment, data were collected by capturing 80 images at half-second intervals as the guide wire moved axially at a speed of 20 mm/s through a phantom model measuring \(100\,\text{mm} \times 100\,\text{mm}\) (see Fig. 3). The phantom includes three circles of different radii positioned at various locations, enabling us to observe and analyze the wire’s deformation under dynamic conditions.
2.3 Optimization problem
Our objective is to replicate the images obtained from the experimental setup described in Sect. 2.2 by solving the differential equations outlined in Sect. 2.1. We focus on two degrees of freedom: the wire’s density, ρ, and the elastic Young’s modulus, E, while assuming that all other parameters are known. Thus, our task is to estimate the MAP of the inverse problem by minimizing the objective function (3), where the parameter vector is \(u = (\rho , E)^{T} \in \mathbb{R}^{d} \) with \(d = 2\).
Once the Cosserat rod ordinary differential equations (ODEs) described in Sect. 2.1 are solved, we must also perform image segmentation to determine the rod’s final position, as the data y is provided in the form of images. We divide the forward modeling process into two main steps:
-
1.
Fix one end position of the rod and solve the Cosserat rod model for the application of a constant force on the other end of the rod up until a fixed time \(t_{\text{end}}\), given the parameter \(u\in \mathbb{R}^{d}\).
We define:
$$\begin{aligned} \mathcal{E}:\mathbb{R}^{d}&\to \mathbb{R}\times \mathbb{R}^{3} \\ x&\mapsto \left (r(s,t),Q(s,t)\right ), \end{aligned}$$where \(s\in \left [0,L\right ], t\in \left [0,t_{\text{end}}\right ], r(s,t)\) describes the center line at position s and time t and \(Q(s,t)\) describes the orientation frame.
-
2.
Image segmentation: this part consists of the following steps
-
(a)
We depict the last position of the rod as an image in 2D space, i.e., define
$$\begin{aligned} f_{\text{img}}:\mathbb{R}\times \mathbb{R}^{3}&\to \left (\mathbb{R}^{d_{x} \times d_{y}}\right )^{3} \\ \left (r(s,t_{\text{end}}),Q(s,t_{\text{end}})\right )&\mapsto f_{ \text{img}}\left (r(s,t_{\text{end}}),Q(s,t_{\text{end}})\right ), \end{aligned}$$here each element represents a pixel of the image, that consists of the RGB-values.
-
(b)
Convert frames into greyscale image. Define
$$\begin{aligned} f_{\text{RGBtoGREY}}:\left (\mathbb{R}^{d_{x}\times d_{y}}\right )^{3}& \to \{0,1,\ldots,255\}^{d_{x}\times d_{y}} \\ x&\mapsto f_{\text{RGBtoGREY}}(x). \end{aligned}$$\(f_{\text{RGBtoGREY}}\) assigns each pixel, based on its shade, a number between 0 and 255, where 0 represents the color black and 255 the color white.
-
(c)
Transform the greyscale images into binary images via a threshold function, i.e., define
$$\begin{aligned} f_{\text{thresh},\sigma}:\{0,1,\ldots,255\}^{d_{x}\times d_{y}}&\to \{0,255 \}^{d_{x}\times d_{y}} \\ x_{i,j}&\to \textstyle\begin{cases} 0,\quad &\text{if } x_{i,j}\leq \sigma \\ 255,\quad &\text{if } x_{i,j}>\sigma \end{cases}\displaystyle , \end{aligned}$$where \(\sigma \in \{1,2,\ldots,255\}\) indicates whether pixels are turned black (\(\left (f_{\text{thresh},\sigma}(x)\right )_{i,j}=0\)) or white (\(\left (f_{\text{thresh},\sigma}(x)\right )_{i,j}=255\)).
-
(d)
Distance transformation: Define
$$\begin{aligned} f_{\text{dist}}:\{0,255\}^{d_{x}\times d_{y}}&\to \mathbb{R}^{d_{x} \cdot d_{y}} \\ x&\mapsto f_{\text{dist}}(x). \end{aligned}$$Here \(f_{\text{dist}}\) computes the distance of each white pixel to the nearest black pixel. The exact method to compute the distance can be found in [14]. To conclude the segmentation we vectorize the image.
-
(a)
We denote the composition of the operators as \(\mathcal{F}=f_{\text{dist}}\circ f_{\text{thresh},\sigma}\circ f_{ \text{RGBtoGREY}}\circ f_{\text{img}}\). Then \(G:=\mathcal{F}\circ \mathcal{E}\), denotes the forward operator in the potential (3). It is important to note that, in order to minimize the potential function, a distance transformation must also be applied to the original image. The following example demonstrates one of the cases we consider.
Example 1
Fig. 4 shows an example of an original image where a force has been applied to the rod. Afterward, we apply the image segmentation process, denoted by \(\mathcal{F} \), to this image. The final result is a distance transformation of the image, which represents our observed data y that we aim to reconstruct. A distance map of a simplified example is illustrated in Fig. 5.
3 Ensemble Kalman inversion (EKI)
We aim to find the minimizer of (3) using EKI, focusing on the continuous version as introduced in [27].
Let \(u_{0} = (u_{0}^{(j)})_{j \in J} \in X^{{N_{\mathrm{ens}}}}\) denote the initial ensemble, where we assume, without loss of generality, that the family \((u_{0}^{(j)} - \bar{u}_{0})_{j \in J}\) is linearly independent. Here, \({N_{\mathrm{ens}}}\in \mathbb{N}\) represents the number of ensemble members, with \({N_{\mathrm{ens}}}\geq 2\), and \(J := \{1, \ldots , {N_{\mathrm{ens}}}\}\) is the index set.
We adopt an EKI approach without a stochastic component, where the particles are determined by solving the following system of ordinary differential equations (ODEs).
where \(\widehat{C}^{u G}_{t}\) is defined as
and \(\overline{u}(t)\) is given by
It has been shown, that the continuous variant (6) corresponds to a noise free limit for \(t\to \infty \), i.e. overfitting will occur in the noisy case. Therefore, we include an additional regularization term
with
In the nonlinear setting, controlling the mean in the observation space through variance inflation has been shown to be essential for managing nonlinearity; see [35] for more details. The dynamics in this context are then given by
where \(0\leq \rho < 1\). We can rewrite this as
Remark 1
Note that, since Γ is positive definite we can multiply (1) by the inverse square root of Γ and not change the predicted solution. For the sake of simplicity and without loss of generality, we will assume that Γ is the identity matrix \(\mathrm{Id}_{k}\).
3.1 Convergence analysis of EKI
As a basis for the convergence analysis of the subsampling techniques in the nonlinear setting, we summarize the properties of EKI based on [35].
Assumption 1
The functional  satisfies
satisfies
-
1.
(μ-strong convexity). There exists \(\mu >0\) such that
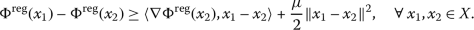
-
2.
(L-smoothness). There exists \(L>0\) such that the gradient
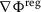 satisfies:
satisfies: 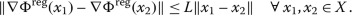
Furthermore, we assume
Assumption 2
The forward operator \(G\in C^{2}(X,Y)\) is locally Lipschitz continuous, with constant \(c_{lip}>0\) and satisfies
where DG denotes the Fréchet derivative of G. Furthermore, the approximation error is bounded by
To understand the dynamics of the EKI, we begin by discussing the subspace property, which indicates that the EKI estimates are constrained to the span of the initial ensemble \(S={\mathrm{span}}\{u^{(j)}, j\in \{1,\ldots ,J\}\}\). Specifically, the particles remain within the affine space \(u_{0}^{\perp }+ \mathcal{E}\) for all \(t \ge 0\), as detailed in [9, Corollary 3.8]. Here, \(\mathcal{E}\) is defined as the span of vectors, i.e., \(\mathcal{E}:=\{e^{(1)}(0), \ldots , e^{({N_{\mathrm{ens}}})}(0)\}\), where \(e^{(j)} = u^{(j)} - \bar{u}\) for \(j \in \{1, \ldots , {N_{\mathrm{ens}}}\}\), and \(u_{0}^{\perp }= \bar{u}(0) - P_{\mathcal{E}} \bar{u}(0)\). We define \(\mathcal{B}:= u_{0}^{\perp }+ \mathcal{E}\).
Theorem 3
([35])
Let \(\{u^{(1)}(0),\ldots,u^{(J)}(0)\}\) denote the initial ensemble. The ODE systems (7) and (8), admit unique global solutions \(u^{(j)}(t)\in C^{1}([0,\infty );\mathcal{B})\) for all \(j\in \{1,\ldots,J\}\).
Therefore, the best possible solution that we can obtain through the EKI is given by best approximation in \(u_{0}^{\perp }+\mathcal {E}\). We summarize in the following the convergence results for the various variants.
Theorem 4
([35])
Suppose Assumptions 1and 2are satisfied. Furthermore we define \(V_{e}(t)=\frac{1}{J}\sum _{j=1}^{J}\frac{1}{2}\|e^{(j)}_{t}\|^{2}\), where \(e^{(j)}_{t}=u^{(j)}_{t}-\bar{u}_{t}\). Let \(j\in \{1,\ldots,J\}\) and \(u^{(j)}(t)\) be the solutions of (7) (or respectively (8)) then it holds
-
1.
The rate of the ensemble collapse is given by
$$ V_{e}(t) \in \mathcal {O}(t^{-1}). $$ -
2.
The smallest eigenvalue of the empirical covariance matrix \(\widehat{C}^{u}_{t}\) remains strictly positive in the subspace \(\mathcal{B}\), i.e. let
$$ \eta _{0} = \min _{z\in B, \|z\|=1}\langle z,C(u_{0}),z\rangle >0. $$Then it holds for each \(z\in \mathcal{B}\) with \(\|z\|=1\)
$$ \langle z, \widehat{C}(u_{t})z\rangle \ge \frac{1}{(1-\rho )mt+\eta _{0}}, $$where \(m>0\) depends on the eigenvalues of \(\widehat{C}^{u}_{0}\) and Γ and the Lipschitz constant \(c_{lip}\) and \(0\leq \rho <1\).
-
3.
Let \(u^{*}\) be the unique minimiser of (3) in \(\mathcal{B}\) then it holds
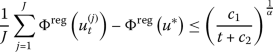
where \(0<\alpha <(1-\rho )\frac{L}{\mu}(\sigma _{max}+c_{lip}\lambda _{max} \|C_{0}\|_{HS})\). Here \(\sigma _{max}\) denotes the largest eigenvalue of \(C_{0}^{-1}\), \(\lambda _{max}\) denotes the larges eigenvalue of \(\Gamma ^{-1}\), \(\|C_{0}\|_{HS}\) denotes the Hilbert-Schmidt norm, \(0\leq \rho <1\) and \(c_{1},c_{2}>0\) depends on the constants from our assumptions 1and 2.
4 Subsampling in EKI
If \({N_{\mathrm{obs}}}\) is very large, as it will be the case for high-resolution images, it might be computationally infeasible to use the EKI framework to solve the inverse problem (1). Therefore, we employ a subsampling strategy. This strategy involves splitting the data y into \({N_{\mathrm{sub}}}\) subsets, denoted as \(y_{1},\ldots ,y_{{N_{\mathrm{sub}}}}\), where \((y_{1},\ldots ,y_{{N_{\mathrm{sub}}}})^{T} = y, {N_{\mathrm{sub}}}\in \{2,3,\ldots \}\) and we use an index set \(I := \{1,\ldots ,{N_{\mathrm{sub}}}\}\) to represent these subsets. We define “data subspaces” \(Y_{1},\ldots , Y_{{N_{\mathrm{sub}}}}\) to accommodate this data partitioning, resulting in \(Y := \prod _{i \in I} Y_{i}\). Regarding the noise we assume the existence of covariance matrices \(\Gamma _{i} : Y_{i} \rightarrow Y_{i}\), for each \(i \in I\), which collectively form a block-diagonal structure within Γ:
Finally, we split the operator G into a family of operators \((G_{i})_{i \in I}\) obtaining the family of inverse problems
where \(\eta _{i}\) is a realisation of the a Gaussian random variable with zero-mean and covariance matrix \(\Gamma _{i}\).
Similar to above we assume \(\Gamma _{i}\) is the identity matrix \(\mathrm{Id}_{ki}\) for the remaining discussion. Then for our analysis we consider the family of potentials
When adding regularization we can define the following entities to obtain a compact representation. We set \(C_{0}=\frac{{N_{\mathrm{sub}}}}{\alpha}D_{0}\) and define
Then we obtain the family of regularized potentials

Note that we scale the regularization parameter by \({N_{\mathrm{sub}}}^{-1}\) so that we obtain

We will consider the right hand sides of the ODEs (7) and (8) but replace G with \(G_{i}\) and respectively y with \(y_{i}\) randomly. This method was introduced in [18] and is known as single-subsampling. We illustrate the idea in Fig. 6. For the analysis of the subsampling scheme, we will assume the same convexity assumptions on the sub-potentials \(\Phi _{i}\) as well as the same regularity assumptions on the family of forward operators \(G_{i}\) for all \(i\in I\).
Illustration of EKI with subsampling. Here we took the distance transformation from image 4 and split the image horizontally into four subimages. Then at each time point where the data is changed, the particles see a different image until the next time when the data is changed
Assumption 5
The families of potentials \((\Phi _{i},i\in I)\) and \((G_{i},i\in I)\) satisfy assumptions 1 and 2.
Then the flows that we are going to consider are given by
when we only consider regularization. In case of variance inflation we consider
where \(0\leq \rho < 1\). Here \({{\boldsymbol{i}}(t)}\) denotes an index process that determines which subset we are considering at which time points. The analysis of subsampling in continuous time as well as the definition of the index process will be introduced in the following Sect. 4.1, where we summarize the results of [24]. Note that the empirical covariance in case of subsampling is given by
4.1 Convergence analysis of EKI with subsampling
To determine which subsample we use, when solving the EKI, we consider a continuous-time Markov process (CTMP) \({\boldsymbol{i}}: [0, \infty ) \times \Omega \rightarrow I\) on I. This process is a piecewise constant process that randomly changes states at random times given by the distribution of Δ. The CTMP has initial distribution \({\boldsymbol{i}}(0) \sim \mathrm{Unif}(I)\) and transition rate matrix
where \(\eta : [0, \infty ) \rightarrow (0, \infty )\) is the learning rate, which is continuously differentiable and bounded from above.
Algorithm 1 describes how we sample from \(({\boldsymbol{i}}(t))_{t \geq 0}\).
For a more detailed analysis of this particular CTMP \(({\boldsymbol{i}}(t))_{t \geq 0}\) we refer to [24]. For other characterisations we refer the reader to [1, 17].
Next we define a stochastic approximation process.
Definition 1
Let \((\mathbf{F}_{i},i \in I): X \times [0, \infty ) \rightarrow X\) be a family Lipschitz continuous functions. Then the tuple \(({\boldsymbol{i}}(t), u(t))_{t \geq 0}\) consisting of the family of flows \((\mathbf{F}_{i})_{i \in I}\) and the index process \(({\boldsymbol{i}}(t))_{t \geq 0})\) that satisfies
is defined as stochastic approximation process.
Furthermore, we define \({\overline{\mathbf{F}}}= \sum _{i \in I}\mathbf{F}_{i}/{{N_{\mathrm{sub}}}}\) and introduce the flow
To analyse the asymtotic behaviour of the process we need the following:
Assumption 6
Let \(d \in \mathbb{N}\) and assume for any \(i \in I\):
-
(i)
\(\mathbf{F}_{i} \in C^{1}(X\times [0, \infty ),X)\),
-
(ii)
there exists a measurable function \(h: [0, \infty ) \rightarrow \mathbb{R}\), with \(\int _{0}^{\infty }h(t) \mathrm{d}t = \infty \) such that the flow \(\varphi _{t}^{(i)}\) satisfies
$$ \langle \mathbf{F}_{i}(\varphi _{t}^{(i)}(u_{0}),t)- \mathbf{F}_{i}( \varphi _{t}^{(i)}(u_{1}),t), \varphi _{t}^{(i)}(u_{0}) - \varphi _{t}^{(i)}(u_{1}) \rangle _{X} \leq -h(t) \| \varphi _{t}^{(i)}(u_{0}) - \varphi _{t}^{(i)}(u_{1}) \|^{2} $$for any two initial values \(u_{0}, u_{1} \in X\).
By Assumption 6(ii) we obtain that the flow of \(-{\overline{\mathbf{F}}}\) is exponentially contracting. Hence, by the Banach fixed-point Theorem, the flow has a unique stationary point \(u^{*} \in X\). The main result of [24] shows that the stochastic process converges to the unique stationary point \(u^{*}\) of the flow \((\overline{\varphi}_{t})_{t \geq 0}\) and is summarized below.
Theorem 7
Consider the stochastic approximation process \(({\boldsymbol{i}}(t), u(t))_{t \geq 0}\), which is initialised with \((i_{0}, u_{0}) \in I \times X\). Furthermore, let Assumption 6hold and that the learning rate satisfies, \(\lim _{t \rightarrow \infty}\eta (t) = 0\). Then
where \(\mathrm{d}_{\mathrm{W}}\) denotes the Wasserstein distance, i.e.
where \(q \in (0,1]\) and \(C(\pi , \pi ')\) denotes the set of couplings of the probability measures \(\pi , \pi '\) on \((X, \mathcal{B}X)\).
For the proof we refer to [18, Theorem A.1].
To analyse convergence of our subsampling scheme we verify that the gradient flow satisfies Assumption 6. Then the result follows by Theorem 7. Condition \((ii)\) is hereby essential. We consider the scaled left hand side
for t large enough, where \(- \mathbf{F}_{i}(u(t),t)\) denotes the right hand side of the systems (12) and (13) and \(h: [0, \infty ) \rightarrow \mathbb{R}\) being a measurable function. In order to derive convergence results in the parameter space, we will focus in the following on the regularized setting, i.e. we consider the potential  and only consider the variance inflated flow (13).
and only consider the variance inflated flow (13).
Theorem 8
Let Assumption 5be satisfied and \({N_{\mathrm{ens}}}>d\). Furthermore, let \(({\boldsymbol{i}}(t))_{t \geq 0})\) be an index process and assume \((u^{(j)}(t))_{t \geq 0, j \in J}\) satisfies (12) (or respectively (13)), and \(\alpha >2\) in Theorem 4. Then the stochastic approximation process \(({\boldsymbol{i}}(t), u^{(j)}(t))_{t \geq 0, j \in J}\) satisfies
Proof
Note that we obtain (12) from (13) by choosing \(\rho =0\), thus, we will focus on (13).
Let \(u_{1}\) and \(u_{2}\) be two coupled process with initial values \(u_{1}(0),u_{2}(0)\). We want to show the existence of a function \(h: [0, \infty ) \rightarrow \mathbb{R}\) with \(\int _{0}^{\infty }h(t) \mathrm{d}t = \infty \) such that
Note that due to the strong convexity of  we obtain from Theorem 4\(u^{(j)}\to u^{*}\) with rate \(\mathcal{O}(t^{-\frac{1}{\alpha}})\), i.e.
we obtain from Theorem 4\(u^{(j)}\to u^{*}\) with rate \(\mathcal{O}(t^{-\frac{1}{\alpha}})\), i.e.
Furthermore, by Theorem 4 we also obtain that  is bounded, i.e., there exists a \(B>0\) such that
is bounded, i.e., there exists a \(B>0\) such that

Since \(u_{1}\) and \(u_{2}\) are column vectors consisting of the stacked particle vectors we need to introduce new variables to represent (13) in vectorized notion. We define for all \(i\in \{1,\ldots,{N_{\mathrm{sub}}}\}\) the operators \(\mathcal{G}_{i}:X^{J}\rightarrow \mathbb{R}^{d\times J}\), \(u\to \left [G_{i}(u),\ldots,G_{i}(u)\right ]^{T}\in \mathbb{R}^{k{N_{ \mathrm{ens}}}}\) and \(\bar{\mathcal{G}_{i}}:X^{J}\rightarrow \mathbb{R}^{k{N_{\mathrm{ens}}}}\), \(u\to \left [\bar{G_{i}}(u),\ldots,\bar{G_{i}}(u)\right ]^{T}\in \mathbb{R}^{k{N_{\mathrm{ens}}}}\), Moreover, we set \(\mathbf{\widehat{C}_{u}}=diag\{\widehat{C}_{u},\widehat{C}_{u},\ldots, \widehat{C}_{u}\}\in \mathbb{R}^{d{N_{\mathrm{ens}}}\times d{N_{\mathrm{ens}}}}, \mathbf{\widehat{C}^{uG}_{i}}=diag\{\widehat{C}^{uG}_{i},\widehat{C}^{uG}_{i},\ldots, \widehat{C}^{uG}_{i}\}\in \mathbb{R}^{d{N_{\mathrm{ens}}}\times d{N_{\mathrm{ens}}}}, \mathbf{C_{0}^{-1}}=diag\{C_{0}^{-1},C_{0}^{-1},\ldots,C_{0}^{-1}\}\in \mathbb{R}^{d{N_{\mathrm{ens}}}\times d{N_{\mathrm{ens}}}}\) and \(\mathbf{y_{i}}=\left [y_{i},y_{i},\ldots ,y_{i}\right ]^{T}\in \mathbb{R}^{k{N_{\mathrm{ens}}}}\). For the potential we define
Thus, we have
We will focus for now on (15) and (16). Equations (17) and (18) can be analysed similarly.
We exploit in the following the fact that we can estimate the difference of the EKI flow to a preconditioned gradient flow. Adding \(-\mathbf{\widehat{C}^{u_{1}}}\nabla \boldsymbol{\Phi}_{i}(u_{1})+ \mathbf{\widehat{C}^{u_{1}}}\nabla \boldsymbol{\Phi}_{i}(u_{1})\) and \(-\mathbf{\widehat{C}^{u_{2}}}\nabla \boldsymbol{\Phi}_{i}(u_{2})+ \mathbf{\widehat{C}^{u_{2}}}\nabla \boldsymbol{\Phi}_{i}(u_{2})\) yields
The first term satisfies
Next we use a result from [35, Lemma 4.5]. With this we can bound the second norm and obtain
Respectively we can do the same for the third term.
For the second and fourth term we obtain

To bound the term

we take a mean-field approach [2, 15], i.e. under suitable assumptions, the sample covariance has a well-defined limit \(C(t)\), where \(C(t)\) is symmetric, positive definite for all \(t\ge 0\). Thus, by splitting

the factor \((I-(\mathbf{\widehat{C}^{u_{1}}})^{-1}\mathbf{\widehat{C}^{u_{2}}})\) can be made arbitrarily small by adjusting \({N_{\mathrm{ens}}}\). We therefore assume, that \({N_{\mathrm{ens}}}\) is chosen large enough such that this term is negligible. Then by μ-strong convexity we obtain the following upper bound for the first term

since \(\lambda _{min}(\widehat{C}^{u_{1}})\in \mathcal{O}\left (t^{-1} \right )\) by Theorem 4. Moreover, since \(\alpha >2\), we have \(-\frac{2+\alpha}{\alpha}>-\frac{3\alpha +2}{2\alpha}\) and therefore the term (19) converges faster then the latter term.
The terms (17) and (18) can be bounded using the similar arguments. The upper bound for these two together is
All together we obtain
where \(h(t)=\frac{\mu}{{N_{\mathrm{ens}}}}\lambda _{min}(\widehat{C}^{u_{1}})\) with \(\int _{0}^{\infty }h(t) \mathrm{d}t = \infty \), since \(\lambda _{min}(\widehat{C}^{u_{1}})\in \mathcal{O}\left (t^{-1} \right )\). □
5 Numerical experiments
We consider the image given in Example 1 for the reconstruction and use the EKI (8) and the suggested EKI with subsampling scheme (13) to estimate the unknown parameters (density ρ and energy dissipation E as discussed in Sect. 2.3), i.e. \(d=2\). To ensure that the EKI is searching a solution in the full space \(\mathbb{R}^{d}\) we consider \({N_{\mathrm{ens}}}=3\). Furthermore, we represent the image as \(705\times 555\) pixel image, this means that the observation space is given by \(Y=\mathbb{R}^{705\times 555}\). We solve the ODEs (8) and (13) up until time \(T=10000\) with \(\rho =0\) in (8) and respectively (13). For the subsampling strategy a linear decaying learning rate \(\eta (t)=(at+b)^{-1}\), where \(a=b=10\) is considered. To account for the minimal step size of the ODE solver, the learning rate \(\eta (t)\) only considered until time \(T_{\text{sub}}=10\). Afterwards we consider a fixed amount of switching times. This results in approximately 600 data switches until time \(T_{\text{sub}}=10\). For the remaining time we switched the data 1000 times. Furthermore, we split the data horizontally into \({N_{\mathrm{sub}}}=5\) subsets.
Figure 7 depicts the mean residuals of the solutions obtained by the EKI and our subsampling scheme. We can see that asymptotically both methods converge with the same rate. However, keep in mind the subsampling approach is computationally cheaper, since we only need to consider the lower-dimensional ODE (13) at each point in time.
Figure 8 depicts the computed solutions in comparison to the original image. We can see that the solutions computed from both methods approximate the rod in the original image quite well. One can see that the desired solution seems to be more elastic than the solutions computed via the EKI and our subsampling approach, which is due to model error.
Comparison of the best computed solutions to the original image. The blue rod depicts the rod from the original image. The thinner rods depict the solutions computed via the EKI (upper rod) and our subsampling approach (lower rod). The right image illustrates the EKI solution (upper rod) and the subsampling solution (lower rod). The x and y axis represent the pixels of the image
Remark 2
We note that the initial idea of our subsampling approach was to ensure feaibility of the EKI in case of large data sets. Indeed, due to the large amount of data the required memory space can often be not large enough for numerical computations. The effective data space that is used in the subsampling approach reduces to \({N_{\mathrm{obs}}}/{N_{\mathrm{sub}}}\). Furthermore, due to the smaller data sets that are used in the computations, each particle also works with smaller data dimensions which can lead to a decrease of the computation time, depending on the implementation.
6 Conclusions
We have introduced a formulation of a guide wire system with estimation of the unknown parameters by a subsampling version of EKI using high resolution images as data. The experiment with real data shows promising results; the subsampling strategy could achieve a good accuracy while reducing the computational costs significantly. In future work, we will explore this direction further to enable uncertainty quantification in the state estimation, thus making a robust control of the guide wire possible.
Data availability
Data for the conducted numerical experiments is available in the repository: https://github.com/matei1996/EKI_subsampling_guidewire.
References
Anderson W. Continuous-time Markov chains: an applications-oriented approach. Applied probability. Berlin: Springer; 1991.
Armbruster D, Herty M, Visconti G. A stabilization of a continuous limit of the ensemble Kalman inversion. SIAM J Numer Anal. 2022;60(3):1494–515. https://doi.org/10.1137/21M1414000.
Bergemann K, Reich S. A localization technique for ensemble Kalman filters. Q J R Meteorol Soc. 2009;136:701–7. https://doi.org/10.48550/ARXIV.0909.1678.
Bergemann K, Reich S. A mollified ensemble Kalman filter. Q J R Meteorol Soc. 2010;136(651):1636–43. https://doi.org/10.1002/qj.672.
Blömker D, Schillings C, Wacker P, Weissmann S. Well posedness and convergence analysis of the ensemble Kalman inversion. Inverse Probl. 2019;35(8):085007. https://doi.org/10.1088/1361-6420/ab149c.
Blömker D, Schillings C, Wacker P, Weissmann S. Continuous time limit of the stochastic ensemble Kalman inversion: strong convergence analysis. SIAM J Numer Anal. 2021;60(6):3181–215. https://doi.org/10.48550/ARXIV.2107.14508.
Bungert L, Wacker P. Complete deterministic dynamics and spectral decomposition of the linear ensemble Kalman inversion. 2021. https://doi.org/10.48550/ARXIV.2104.13281
Calvello E, Reich S, Stuart AM. Ensemble Kalman methods: a mean field perspective. 2022. https://doi.org/10.48550/ARXIV.2209.11371.
Chada NK, Stuart AM, Tong XT. Tikhonov regularization within ensemble Kalman inversion. SIAM J Numer Anal. 2020;58(2):1263–94. https://doi.org/10.1137/19M1242331.
Choromanska A, Henaff M, Mathieu M, Arous GB, LeCun Y. The loss surfaces of multilayer networks. J Mach Learn Res. 2014;38:192–204. https://doi.org/10.48550/ARXIV.1412.0233.
Dashti M, Law KJH, Stuart AM, Voss J. Map estimators and their consistency in Bayesian nonparametric inverse problems. Inverse Probl. 2013;29(9):095017. https://doi.org/10.1088/0266-5611/29/9/095017.
Ding Z, Li Q. Ensemble Kalman inversion: mean-field limit and convergence analysis. Stat Comput. 2020;31(9).
Evensen G. The Ensemble Kalman filter: theoretical formulation and practical implementation. Ocean Dyn. 2003;53(4):343–67. https://doi.org/10.1007/s10236-003-0036-9.
Felzenszwalb PF, Huttenlocher DP. Distance transforms of sampled functions. Theory Comput. 2012;8(19):415–28. https://doi.org/10.4086/toc.2012.v008a019.
Garbuno-Inigo A, Hoffmann F, Li W, Stuart AM. Interacting Langevin diffusions: gradient structure and ensemble Kalman sampler. SIAM J Appl Dyn Syst. 2020;19(1):412–41. https://doi.org/10.1137/19M1251655.
Gazzola M, Dudte LH, McCormick AG, Mahadevan L. Forward and inverse problems in the mechanics of soft filaments. R Soc Open Sci. 2018;5(6):171628. https://doi.org/10.1098/rsos.171628.
Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81(25):2340–61. https://doi.org/10.1021/j100540a008.
Hanu M, Latz J, Schillings C. Subsampling in ensemble Kalman inversion. Inverse Probl. 2023;39(9):094002. https://doi.org/10.1088/1361-6420/ace64b.
Iglesias MA. Iterative regularization for ensemble data assimilation in reservoir models. Comput Geosci. 2014;19:177–212. https://doi.org/10.48550/ARXIV.1401.5375.
Iglesias MA. A regularizing iterative ensemble Kalman method for PDE-constrained inverse problems. Inverse Probl. 2016;32(2):025002. https://doi.org/10.1088/0266-5611/32/2/025002.
Iglesias MA, Law KJH, Stuart AM. Ensemble Kalman methods for inverse problems. Inverse Probl. 2013;29(4):045001. https://doi.org/10.1088/0266-5611/29/4/045001.
Jin K, Latz J, Liu C, Schönlieb C. A continuous-time stochastic gradient descent method for continuous data. arXiv:2112.03754 (2021).
Klebanov I, Wacker P. Maximum a posteriori estimators in \(\ell^{p}\) are well-defined for diagonal Gaussian priors. Inverse Probl. 2023;39(6):065009. https://doi.org/10.1088/1361-6420/acce60.
Latz J. Analysis of stochastic gradient descent in continuous time. Stat Comput. 2021;31:39. https://doi.org/10.1007/s11222-021-10016-8.
Li G, Reynolds A. Iterative ensemble Kalman filters for data assimilation. SPE J. 2009;14:496–505. https://doi.org/10.2118/109808-PA.
Robbins H, Monro S. A stochastic approximation method. Ann Math Stat. 1951;22(3):400–7. https://doi.org/10.1214/aoms/1177729586.
Schillings C, Stuart A. Convergence analysis of ensemble Kalman inversion: the linear, noisy case. Appl Anal. 2017;97. https://doi.org/10.48550/ARXIV.1702.07894.
Schillings C, Stuart AM. Analysis of the ensemble Kalman filter for inverse problems. SIAM J Numer Anal. 2016;55(3):1264–90. https://doi.org/10.48550/ARXIV.1602.02020.
Sharei H, Alderliesten T, van den Dobbelsteen JJ, Dankelman J. Navigation of guidewires and catheters in the body during intervention procedures: a review of computer-based models. J Med Imag. 2018;5(01):010902. https://doi.org/10.1117/1.jmi.5.1.010902.
Tekinalp A, Kim SH, Bhosale Y, Parthasarathy T, Naughton N, Nasiriziba I, Cui S, Stölzle M, Shih CHC, Gazzola M. Gazzolalab/pyelastica: v0.3.1 2023. https://doi.org/10.5281/zenodo.7931429.
Tong XT, Majda AJ, Kelly D. Nonlinear stability of the ensemble Kalman filter with adaptive covariance inflation. Commun Math Sci. 2015;14:1283–313. https://doi.org/10.48550/ARXIV.1507.08319.
Tong XT, Majda AJ, Kelly D. Nonlinear stability and ergodicity of ensemble based Kalman filters. Nonlinearity. 2016;29(2):657–91. https://doi.org/10.1088/0951-7715/29/2/657.
Vidal R, Bruna J, Giryes R, Soatto S. Mathematics of deep learning. 2017. https://doi.org/10.48550/ARXIV.1712.04741.
Viellieber R. Simulating guidewires in blood vessels using Cosserat rod theory. Master’s thesis. Ruprecht Karl University of Heidelberg; 2023.
Weissmann S. Gradient flow structure and convergence analysis of the ensemble Kalman inversion for nonlinear forward models. Inverse Probl. 2022;38(10):105011. https://doi.org/10.1088/1361-6420/ac8bed.
Zhang X, Chan FK, Parthasarathy T, Gazzola M. Modeling and simulation of complex dynamic musculoskeletal architectures. Nat Commun. 2019;10(1):4825. https://doi.org/10.1038/s41467-019-12759-5.
Acknowledgements
Not applicable.
Funding
Open Access funding enabled and organized by Projekt DEAL. MH and CS are grateful for the support from MATH+ project EF1-19: Machine Learning Enhanced Filtering Methods for Inverse Problems and EF1-20: Uncertainty Quantification and Design of Experiment for Data-Driven Control, funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – The Berlin Mathematics Research Center MATH+ (EXC-2046/1, project ID: 390685689). The authors of this publication also thank the University of Heidelberg’s Excellence Strategy (Field of Focus 2) for the funding of the project “Ariadne- A new approach for automated catheter control” that allowed the research and development of the control system of the catheter.
Author information
Authors and Affiliations
Contributions
GK designed the forward model and planned the numerical experiments. JM and JS carried out the experimental setup, designing an electrical drive system as well generating data for the numerical experiments. JH designed the data segmentation in the forward model and helped to draft the manuscript. CS introduced and analysed the subsampling scheme for the EKI as well as draft the manuscript. MH introduced and analysed the subsampling scheme for the EKI, carried out the numerical experiments as well as draft the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hanu, M., Hesser, J., Kanschat, G. et al. Ensemble Kalman inversion for image guided guide wire navigation in vascular systems. J.Math.Industry 14, 21 (2024). https://doi.org/10.1186/s13362-024-00159-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13362-024-00159-4





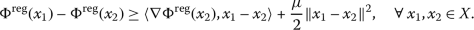
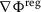 satisfies:
satisfies: